排序算法
如何评价一种排序算法
既然是算法,肯定要分析时间复杂度、空间复杂度。关于时间复杂度是指比较和交换次数,关于空间复杂度是指排序算法申请的额外空间,原地排序就是特指空间复杂度是 O(1) 的排序算法。 另外排序算法还涉及稳定性的评价指标,是指对于比较结果相同的数据,如果每次排序数据顺序都是一样的,那么则是稳定的排序算法,反之则是不稳定的排序算法。
冒泡排序(Bubble Sort)

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置,重复 n 次,就完成了 n 个数据的排序工作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public static void bubbleSort(int[] nums) {
int length = nums.length;
if (length <= 1) {
return;
}
for (int i = 0; i < length; i++) {
boolean flag = false;
for (int j = length - 1; j > i; j--) {
if (nums[j] > nums[j - 1]) {
int tmp = nums[j];
nums[j] = nums[j - 1];
nums[j - 1] = tmp;
flag = true;
}
}
if (!flag) {
break;
}
}
}
|
插入排序(Insertion Sort)

插入排序的算法思想就是,将数组中的数据分已排序区间和未排序区间。初始状态就是数组的第一个元素为已排序区间,右边为未排序区间。依次从未排序区间中取出元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public static void insertionSort(int[] nums) {
int length = nums.length;
if (length <= 1) {
return;
}
for (int i = 1; i < length; i++) {
int value = nums[i];
int j = i - 1;
while (j >= 0) {
if (nums[j] > value) {
nums[j + 1] = nums[j];
j--;
} else {
break;
}
}
nums[j + 1] = value;
}
}
|
选择排序(Selection Sort)

选择排序算法的实现思路有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public static void selectionSort(int[] nums) {
int length = nums.length;
if (length <= 1) {
return;
}
for (int i = 0; i < length; i++) {
int minIdx = i;
for (int j = i; j < length; j++) {
if (nums[minIdx] > nums[j]) {
minIdx = j;
}
}
int tmp = nums[i];
nums[i] = nums[minIdx];
nums[minIdx] = tmp;
}
}
|
归并排序(Merge Sort)
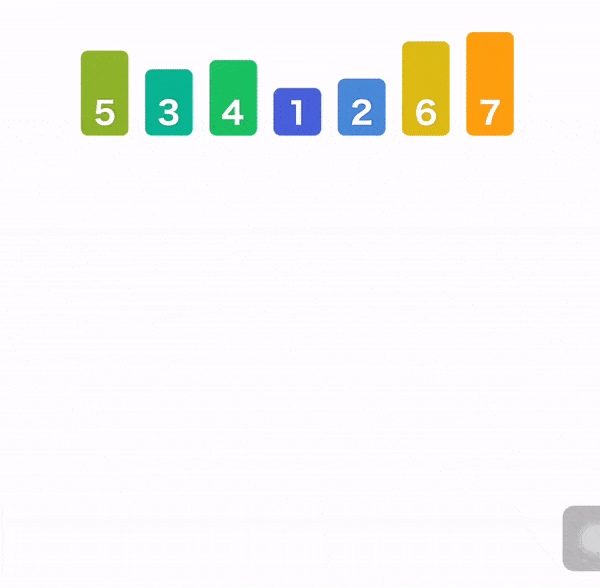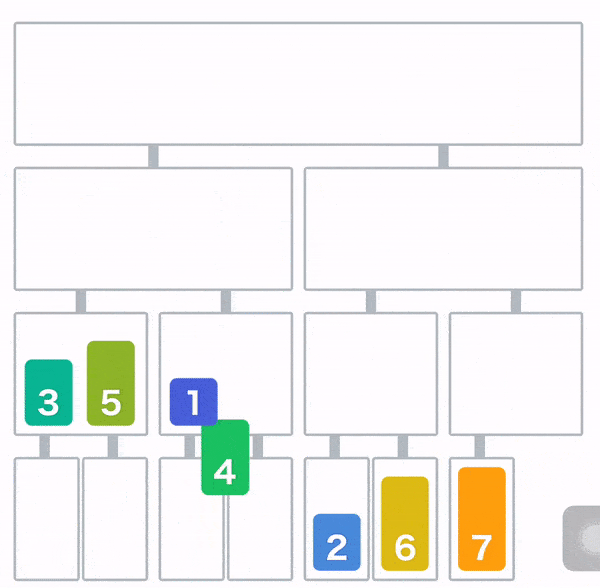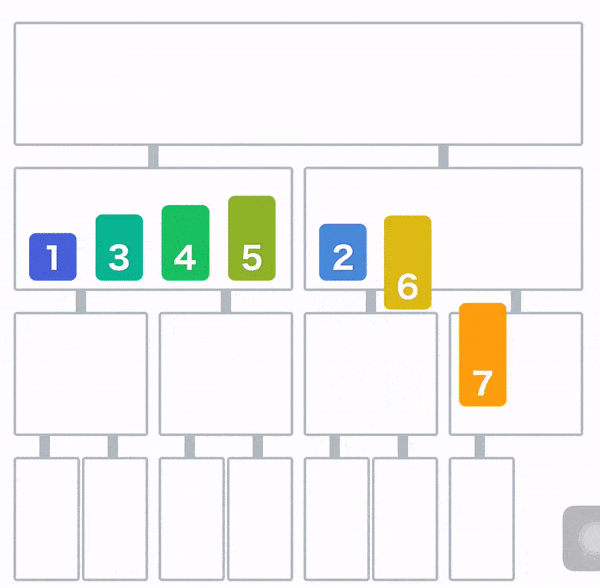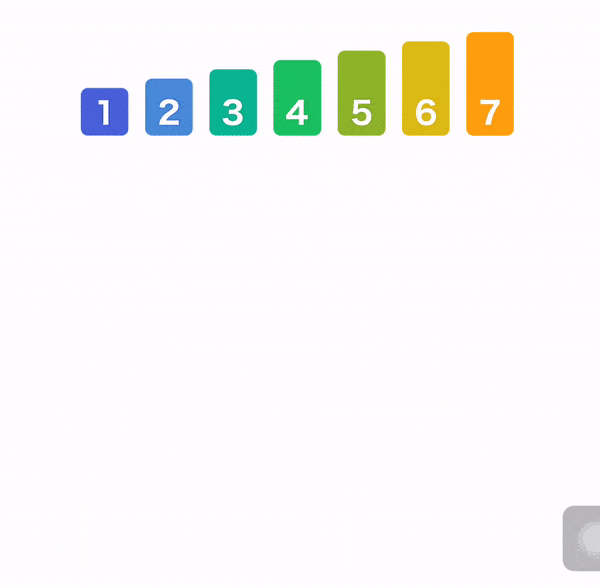
归并排序就使用了分治的思想,先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| public static void mergeSort(int[] nums) {
int length = nums.length;
if (length <= 1) {
return;
}
mergeSort(nums, 0, length - 1);
}
private static void mergeSort(int[] nums, int left, int right) {
if (right <= left) {
return;
}
int mid = (left + right) >> 1;
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
merge(nums, left, mid, right);
}
private static void merge(int[] nums, int left, int mid, int right) {
int[] tmp = new int[right - left + 1];
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
tmp[k++] = nums[i] <= nums[j] ? nums[i++] : nums[j++];
}
while (i <= mid) {
tmp[k++] = nums[i++];
}
while (j <= right) {
tmp[k++] = nums[j++];
}
System.arraycopy(tmp, 0, nums, left, tmp.length);
}
|
快速排序(Quick Sort)

快排也是利用分治的思想,先从数组中取标杆 pivot,将 pivot 小的元素放在 pivot 左边,大的元素放在 pivot 右边,然后依次对右边和右边的子数组继续用同样的方式排序,以达到整个序列有序。图中的例子选取 pivot 是待排数组的最右侧元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| public static void quickSort(int[] nums) {
int length = nums.length;
if (length <= 1) {
return;
}
quickSort(nums, 0, length - 1);
}
private static void quickSort(int[] nums, int left, int right) {
if (left < right) {
int partitionIndex = partition(nums, left, right);
quickSort(nums, left, partitionIndex - 1);
quickSort(nums, partitionIndex + 1, right);
}
}
private static int partition(int[] nums, int left, int right) {
int pivot = right, counter = left;
for (int i = left; i < right; i++) {
if (nums[i] < nums[pivot]) {
int temp = nums[counter];
nums[counter] = nums[i];
nums[i] = temp;
counter++;
}
}
int temp = nums[pivot];
nums[pivot] = nums[counter];
nums[counter] = temp;
return counter;
}
|
堆排序(Heap Sort)
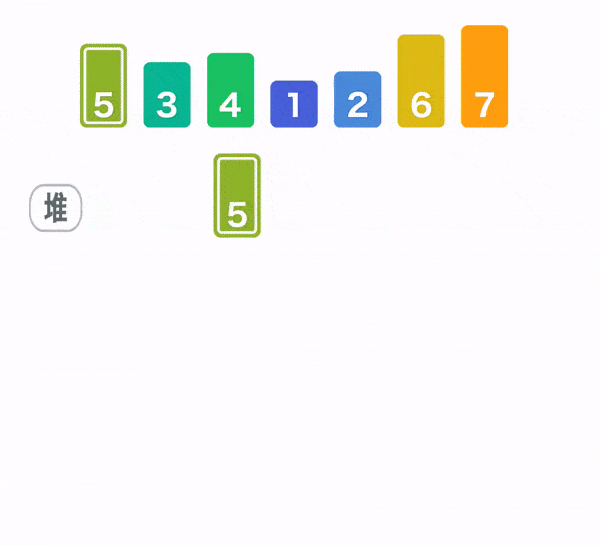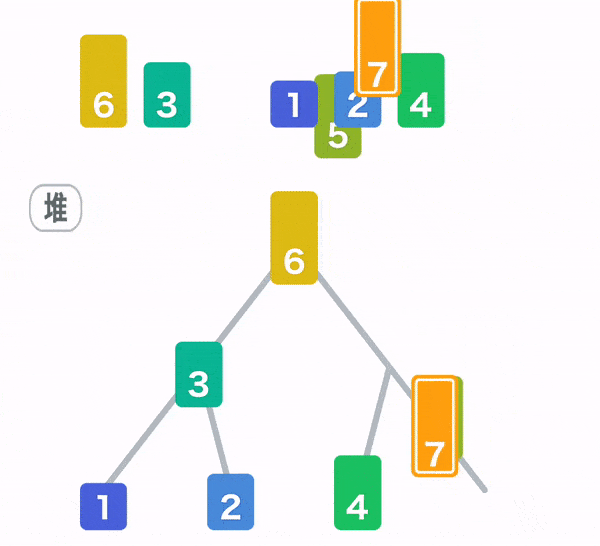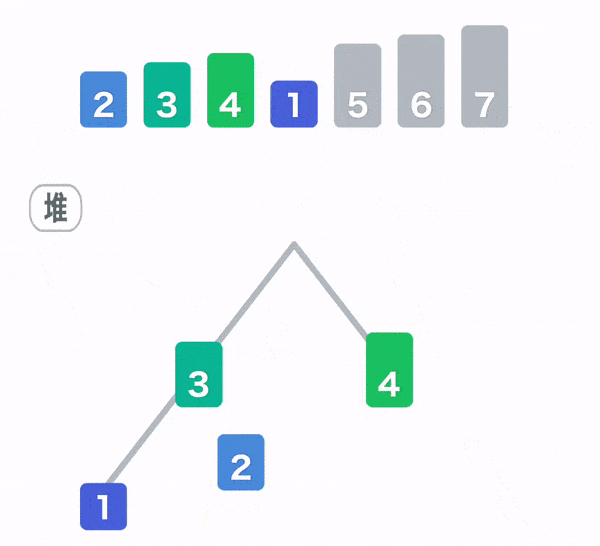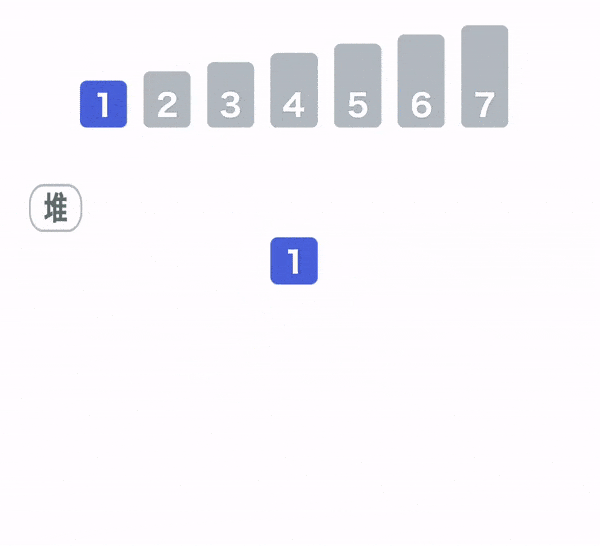
数组元素建立大顶堆,取出堆顶元素和堆尾元素交换,再重新调整成大顶堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
public static void heapSort(int[] nums) {
int length = nums.length;
for (int i = (length - 2) / 2; i >= 0; i--) {
adjustHeap(nums, i, length);
}
for (int i = length - 1; i > 0; i--) {
int temp = nums[0];
nums[0] = nums[i];
nums[i] = temp;
adjustHeap(nums, 0, i);
}
}
public static void adjustHeap(int[] nums, int top, int length) {
int temp = nums[top];
for (int i = 2 * top + 1; i < length; i = i * 2 + 1) {
if (i < length - 1 && nums[i] < nums[i + 1]) {
i++;
}
if (temp > nums[i]) {
break;
}
nums[top] = nums[i];
top = i;
}
nums[top] = temp;
}
|
总结
归并排序和快排都使用来分治的思想,区别是归并排序的处理过程是由下到上的,先处理子问题,然后再合并(merge),而快排正好相反,它的处理过程是由上到下的,先分区(partition),然后再处理子问题。
归并排序虽然时间复杂度很稳定,但是不是原地排序算法,空间复杂度为 O(n),所以它也没有快排应用广泛。快排虽然最坏情况下的时间复杂度是 O(n²),但是平均情况下时间复杂度是 O(nlogn)。而且快排时间复杂度退化到 O(n²) 的概率非常小,我们可以通过合理地选择 pivot 来避免这种情况。
| 排序算法 |
平均时间复杂度 |
最坏时间复杂度 |
最好时间复杂度 |
空间复杂度 |
稳定性 |
| 冒泡排序 |
O(n²) |
O(n²) |
O(n) |
O(1) |
稳定 |
| 选择排序 |
O(n²) |
O(n²) |
O(n²) |
O(1) |
不稳定 |
| 插入排序 |
O(n²) |
O(n²) |
O(n) |
O(1) |
稳定 |
| 快速排序 |
O(nlogn) |
O(n²) |
O(nlogn) |
O(nlogn) |
不稳定 |
| 堆排序 |
O(nlogn) |
O(nlogn) |
O(nlogn) |
O(1) |
不稳定 |
| 希尔排序 |
O(n^1.3) |
O(n²) |
O(n) |
O(1) |
不稳定 |
| 归并排序 |
O(nlogn) |
O(nlogn) |
O(nlogn) |
O(n) |
稳定 |
| 计数排序 |
O(n+k) |
O(n+k) |
O(n+k) |
O(n+k) |
稳定 |
| 基数排序 |
O(n*k) |
O(n*k) |
O(n*k) |
O(n+k) |
稳定 |





